보고 정렬
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
보고 정렬은 무작위로 리스트를 섞는 과정을 반복하여 정렬하는 알고리즘이다. 이 알고리즘은 정렬된 결과가 나올 때까지 계속 섞는 방식으로 작동하며, 의사 코드와 C, C++, Python, Perl, Standard ML 등 다양한 프로그래밍 언어로 구현될 수 있다. 보고 정렬의 평균 비교 횟수는 (e-1)n!이며, 최악의 경우 무한정 실행될 수 있다. 관련 알고리즘으로는 보조 정렬, 고로 정렬, 보고보고 정렬 등이 있다.
더 읽어볼만한 페이지
- 컴퓨터 유머 - 널 장치
널 장치는 Version 5 Unix에서 처음 소개된 특수 파일로, 의도하지 않은 출력 스트림을 버리거나 입력 스트림을 위해 빈 파일 역할을 하며, 유닉스 및 유닉스 계열 운영체제에서 메시지 출력을 제어하는 데 활용된다. - 컴퓨터 유머 - 자곤 파일
자곤 파일은 해커 문화의 속어, 은어, 유머를 모아 놓은 문서이자 사전으로, 라파엘 핀켈에 의해 처음 만들어진 후 여러 해커들에 의해 확장되었으며, 에릭 레이먼드가 편집한 《새로운 해커 사전》은 해커 문화와 기술 분야에 큰 영향을 미쳤다. - 비교 정렬 - 합병 정렬
합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다. - 비교 정렬 - 퀵 정렬
퀵 정렬은 토니 호어가 개발한 분할 정복 방식의 효율적인 정렬 알고리즘으로, 피벗을 기준으로 리스트를 분할하여 정렬하는 과정을 재귀적으로 반복하며 다양한 최적화 기법과 변형이 존재한다. - 정렬 알고리즘 - 합병 정렬
합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다. - 정렬 알고리즘 - 퀵 정렬
퀵 정렬은 토니 호어가 개발한 분할 정복 방식의 효율적인 정렬 알고리즘으로, 피벗을 기준으로 리스트를 분할하여 정렬하는 과정을 재귀적으로 반복하며 다양한 최적화 기법과 변형이 존재한다.
| 보고 정렬 | |
|---|---|
| 개요 | |
| 분류 | 정렬 |
| 자료 구조 | 배열 |
| 최악 시간 복잡도 | 무한대 (무작위화 버전), (결정적 버전) |
| 최적화 여부 | 아니오 |
2. 알고리즘 설명
보고 정렬(Bogo sort)은 정렬하려는 리스트의 요소들을 무작위로 섞는 과정을 반복하는 정렬 알고리즘이다. 리스트의 요소들이 우연히 올바른 순서로 정렬될 때까지 이 무작위 섞기 과정을 계속 수행한다.
예를 들어 트럼프 카드 한 묶음을 순서대로 정렬하는 경우를 생각해 볼 수 있다.
# 카드 묶음을 무작위로 섞는다.
# 섞인 카드를 다시 모은다.
# 카드가 순서대로 정렬되었는지 확인한다. 만약 정렬되지 않았다면, 카드가 올바른 순서로 배열될 때까지 1~3번 과정을 반복한다.
즉, 데이터 묶음이 우연히 원하는 순서대로 정렬될 때까지 계속해서 무작위로 섞는 방식과 같다.
2. 1. 의사 코드
보고 정렬의 기본적인 의사 코드는 다음과 같다.영어 표현:
'''while not''' isInOrder(list):
shuffle(list)
- `isInOrder(list)`: 리스트가 정렬되었는지 확인하는 함수
- `shuffle(list)`: 리스트의 순서를 무작위로 섞는 함수
한국어 표현:
(리스트가 정렬될 때)'''까지 반복''':
리스트 '''섞기'''
다른 형태의 의사 코드 표현은 다음과 같다.
'''while''' 리스트 '''가''' 정렬'''되어 있지 않으면''':
shuffle(리스트)
함수 형태로 표현하면 다음과 같다.
'''함수''' 보고_정렬(배열):
'''while''' 배열이 정렬되어 있지 않음:
배열 := 배열의_임의_순열
- `배열의_임의_순열`: 주어진 배열의 요소들을 무작위 순서로 재배열하는 연산
트럼프 카드 묶음을 순서대로 정렬하는 경우를 예로 들어 보고 정렬 알고리즘을 설명할 수 있다.
# 트럼프 52장 묶음을 흩뿌려 섞는다.
# 1장씩 무작위로 다시 모은다.
# 카드가 순서대로 정렬되었는지 확인한다. 만약 정렬되지 않았다면 1~3번 과정을 반복한다.
즉, 보고 정렬은 데이터 묶음을 계속해서 무작위로 섞고, 우연히 원하는 순서대로 정렬될 때까지 기다리는 방식이다.
2. 2. 구현 예시
다음은 다양한 프로그래밍 언어로 구현된 보고 정렬의 예시이다. 주요 예시로는 표준 ML, C, C++, 파이썬, Perl 등이 있으며, 각 언어별 상세 구현 코드는 해당 하위 섹션에서 확인할 수 있다.2. 2. 1. C
C로 구현한 예시는 다음과 같다.#include
#include
#include
// 주어진 배열에 대해 제자리에서 보고 정렬을 수행한다.
static void bogo_sort(int* a, int size);
// 주어진 배열이 정렬되었으면 1을, 그렇지 않으면 0을 반환한다.
static int is_sorted(int* a, int size);
// 주어진 배열을 임의의 순서로 섞는다.
static void shuffle(int* a, int size);
void bogo_sort(int* a, int size) {
while (!is_sorted(a, size)) {
shuffle(a, size);
}
}
int is_sorted(int* a, int size) {
for (int i = 0; i < size-1; i++) {
if (a[i] > a[i+1]) {
return 0;
}
}
return 1;
}
void shuffle(int* a, int size) {
int temp, random;
for (int i = 0; i < size; i++) {
random = (int) ((double) rand() / ((double) RAND_MAX + 1) * size);
temp = a[random];
a[random] = a[i];
a[i] = temp;
}
}
int main() {
// 예시 사용법
int input[] = { 68, 14, 78, 98, 67, 89, 45, 90, 87, 78, 65, 74 };
int size = sizeof(input) / sizeof(*input);
// 의사 난수 생성기 초기화
srand(time(NULL));
bogo_sort(input, size);
// 정렬된 결과: 14 45 65 67 68 74 78 78 87 89 90 98
printf("sorted result:");
for (int i = 0; i < size; i++) {
printf(" %d", input[i]);
}
printf("\n");
return 0;
}
2. 2. 2. C++
cpp#include
#include
template
void 보고소트( RandomIter first, RandomIter last )
{
while( !std::is_sorted( first, last ) )
std::shuffle( first, last, std::default_random_engine() );
}
2. 2. 3. Python
파이썬 3 구현은 다음과 같다.import random
# 이 함수는 배열이 정렬되었는지 확인합니다.
def is_sorted(random_array):
for i in range(1, len(random_array)):
if random_array[i] < random_array[i - 1]:
return False
return True
# 이 함수는 배열이 정렬될 때까지 배열의 요소를 반복적으로 섞습니다.
def bogo_sort(random_array):
while not is_sorted(random_array):
random.shuffle(random_array)
return random_array
# 이 함수는 무작위로 선택된 정수 값으로 배열을 생성합니다.
def generate_random_array(size, min_val, max_val):
return [random.randint(min_val, max_val) for _ in range(size)]
# 무작위로 생성된 배열의 크기, 최소값 및 최대값
size = 10
min_val = 1
max_val = 100
random_array = generate_random_array(size, min_val, max_val)
print("정렬되지 않은 배열:", random_array)
sorted_arr = bogo_sort(random_array)
print("정렬된 배열:", sorted_arr)
이 코드는
data가 파이썬의 내장 list와 같이 단순하고 변경 가능한 배열과 유사한 데이터 구조이며, 그 요소들을 문제없이 비교할 수 있다고 가정한다.2. 2. 4. Perl
perluse List::Util 'shuffle';
sub is_sorted {
for (1 .. $#_) {
return 0 if ($_[$_ - 1] > $_[$_]);
}
return 1;
}
sub bogosort {
until (is_sorted(@_)) {
@_ = shuffle @_;
}
return @_;
}
2. 2. 5. Standard ML
표준 ML의 셔플을 사용한 코드 예는 아래와 같다.```sml
val _ = load "Random";
load "Int";
val rng = Random.newgen ();
fun select (y::xs, 0) = (y, xs)
| select (x::xs, i) = let val (y, xs') = select (xs, i-1) in (y, x::xs') end
| select (_, i) = raise Fail ("Short by " ^ Int.toString i ^ " elements.");
(* Recreates a list in random order by removing elements in random positions *)
fun shuffle xs =
let fun rtake [] _ = []
| rtake ys max =
let val (y, ys') = select (ys, Random.range (0, max) rng)
in y :: rtake ys' (max-1)
end
in rtake xs (length xs) end;
fun bogosort xs comp =
let fun isSorted (x::y::xs) comp = comp(x,y) <> GREATER andalso isSorted (y::xs) comp
| isSorted _ comp = true;
val a = ref xs;
in while(not(isSorted (!a) comp)) do (
a := shuffle (!a)
); (!a) end;
3. 실행 시간 및 종료
정렬할 모든 요소가 서로 다르다면, 보고 정렬의 평균 비교 횟수는 점근적으로 (''e'' − 1)''n''!이고, 평균 교환(섞음) 횟수는 (''n'' − 1)''n''!이다.[19][5] 평균 교환 횟수는 비교 횟수보다 빠르게 증가하는데, 이는 요소들이 순서대로 정렬되어 있지 않다는 사실은 적은 횟수의 비교만으로도 금방 발견되지만, 배열을 섞는 작업 자체는 배열의 크기(''n'')에 비례하기 때문이다.[19][5]
최선의 경우는 주어진 리스트가 이미 정렬된 경우이다. 이때 비교 횟수는 ''n'' − 1번이며, 섞음은 전혀 수행되지 않는다.[19][5]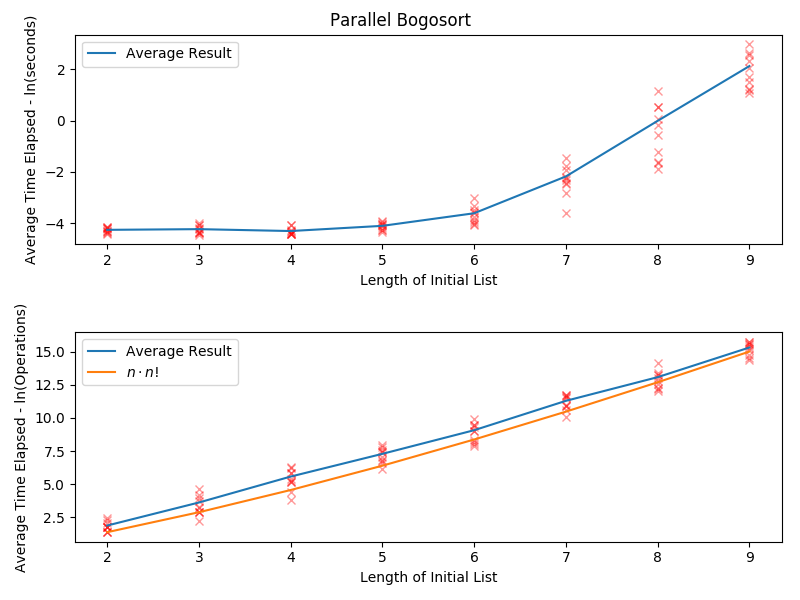
최악의 경우, 비교 및 교환 횟수는 무한할 수 있다. 이는 마치 동전을 던졌을 때 계속 앞면만 나올 수 있는 것처럼, 무작위적인 섞음 과정에서 우연히 정렬된 순서가 영원히 나타나지 않을 수도 있기 때문이다.[19][5]
이론적으로, 고정된 크기의 배열에 대해 이 알고리즘의 예상 런타임은 유한하다. 이는 무한 원숭이 정리와 비슷한 원리로 설명할 수 있는데, 올바른 순열(정렬된 상태)이 나올 확률이 0보다 크기 때문에, 무한히 시도하면 거의 확실히 언젠가는 정렬된 배열을 얻을 수 있기 때문이다.
그러나 실제 컴퓨터에서 유사난수 생성기를 사용하여 섞음을 구현할 경우, 생성되는 난수 배열의 주기성 때문에 특정 순열이 영원히 나타나지 않아 알고리즘이 종료되지 않을 수도 있다.
모든 요소가 서로 다른 경우, 시간 복잡도는 O(n × n!)이다. 이는 한 번의 섞기와 정렬 확인에 O(n) 시간이 걸리고, 평균적으로 n!번의 섞음 시도가 필요하기 때문이다. 만약 배열 내에 동일한 요소가 포함되어 있다면, 올바른 정렬 상태의 가짓수를 ''a''라고 할 때 시간 복잡도는 O(n × n! / ''a'')가 된다.
4. 관련 알고리즘
- '''보조 정렬 (Bozo sort)''': 난수를 기반으로 하는 정렬 알고리즘이다.[5] 리스트가 정렬되어 있지 않으면 무작위로 두 항목을 선택하여 교환한 다음 리스트가 정렬되었는지 확인한다. 보조 정렬의 실행 시간 분석은 더 어렵지만, H. Gruber의 "perversely awful" 무작위 정렬 알고리즘 분석에서 몇 가지 추정치를 찾을 수 있다.[5] 기댓값은 ''O(n!)''이다.
- '''고로 정렬 (Goro sort)''': 2011년 구글 코드잼에서 소개된 정렬 알고리즘이다.[6] 목록이 정렬되지 않은 경우, 모든 요소의 부분 집합이 무작위로 순열된다. 이 부분 집합이 매번 최적으로 선택된다면, 이 연산을 수행해야 하는 총 횟수의 기댓값은 잘못 배치된 요소의 수와 같다.
- '''보고보고 정렬 (Bogo-bogo sort)''': 목록의 시작 부분을 작게 복사하여 재귀적으로 호출하여 정렬되었는지 확인하는 알고리즘이다. 기본 경우는 항상 정렬된 단일 요소이다. 다른 경우, 마지막 요소를 목록의 이전 요소에서 가장 큰 요소와 비교한다. 마지막 요소가 크거나 같으면 복사본의 순서가 이전 버전과 일치하는지 확인하고, 일치하면 반환한다. 그렇지 않으면 목록의 현재 복사본을 섞고 재귀적 확인을 다시 시작한다.[7]
- '''최악 정렬 (Worst sort)''': 유한한 시간 내에 완료가 보장되는 최악의 정렬 알고리즘이다. 그러나 효율성은 구성에 따라 임의로 나빠질 수 있다.[8] 최악정렬 알고리즘은 나쁜 정렬 알고리즘인 나쁜정렬을 기반으로 한다. 나쁜정렬 알고리즘은 두 개의 매개변수, 즉 정렬할 목록인 ''L''과 재귀 깊이인 ''k''를 허용한다. 재귀 레벨 ''k'' = 0에서 나쁜정렬은 일반적인 정렬 알고리즘(예: 버블 정렬)을 사용하여 입력을 정렬하고 정렬된 목록을 반환한다. 즉, 나쁜정렬(''L'', 0) = 버블정렬(''L'')이다. 따라서 나쁜정렬의 시간 복잡도는 ''k'' = 0인 경우 ''O(n2)''이다. 그러나 ''k'' > 0의 경우, 나쁜정렬(''L'', ''k'')은 먼저 ''L''의 모든 순열 목록인 ''P''를 생성한다. 그런 다음 나쁜정렬은 나쁜정렬(''P'', ''k'' - 1)을 계산하고 정렬된 ''P''의 첫 번째 요소를 반환한다. 최악정렬을 진정으로 최악으로 만들기 위해 ''k''는 함수 ''f'': N → N (예: ''f''(''n'') = ''A''(''n'', ''n''))과 같은 계산 가능한 증가 함수 값으로 할당될 수 있다. 여기서 ''A''는 아커만 함수이다. 따라서 목록을 임의로 나쁘게 정렬하려면 최악정렬(''L'', ''f'') = 나쁜정렬(''L'', ''f''(길이(''L''))), 여기서 길이(''L'')는 ''L''의 요소 수이다. 결과 알고리즘의 복잡성은 Ω((n!(''f''(''n'')))2)이며, 여기서 n!(''m'') = (...((n!)!)!...)!는 ''n''의 계승을 ''m''번 반복한 것이다. 이 알고리즘은 충분히 빠르게 증가하는 함수 ''f''를 선택하여 원하는 만큼 비효율적으로 만들 수 있다.[8]
- '''느린정렬 (Slow sort)''': 대규모 복잡성을 달성하기 위해 잘못된 분할 정복 전략을 사용하는 또 다른 유머러스한 정렬 알고리즘이다.
- '''양자 보조 정렬 (Quantum Bogo sort)''': 컴퓨터 과학자들 사이에서 내부 농담으로 만들어진 보조 정렬을 기반으로 하는 가설 정렬 알고리즘이다. 이 알고리즘은 양자 엔트로피 소스를 사용하여 입력의 무작위 순열을 생성하고, 목록이 정렬되었는지 확인한 다음, 정렬되지 않은 경우 우주를 파괴한다. 다세계 해석이 유효하다고 가정하면 이 알고리즘을 사용하면 ''O(n)'' 시간에 입력이 성공적으로 정렬된 최소 하나의 생존 우주가 생성된다.[9]
- '''기적 정렬 (Miracle sort)''': 기적이 일어날 때까지 배열이 정렬되었는지 확인하는 정렬 알고리즘이다. 배열의 순서를 변경하지 않고 정렬될 때까지 지속적으로 배열을 확인한다.[10] 순서가 변경되지 않기 때문에 알고리즘의 가설적인 시간 복잡도는 ''O(∞)''이지만 기적이나 단일 이벤트 오류와 같은 이벤트를 통해 정렬될 수 있다. 이 알고리즘의 구현에 특별한 주의를 기울여야 하는데, 최적화 컴파일러가 이를 while(true) 루프로 변환할 수 있기 때문이다. 그러나 최상의 경우는 정렬된 목록에서 발생하는 ''O(n)''이다. 비교만 수행하므로 제자리 정렬이며 안정적이다.
- '''보조보고 정렬 (Bozobogo sort)''': 목록이 이미 정렬된 경우에만 작동하는 정렬 알고리즘이다. 그렇지 않으면 기적 정렬의 조건이 적용된다.
5. 기타
자르곤 파일의 "보고 정렬" 항목[14]에서는 'A spectacular variant'라는 변형이 제안되었는데, 이는 양자적으로 모든 선택(순열 생성)을 병렬 처리하여 올바른 순서로 정렬된 결과만을 가져오는 아이디어이다.
참조
[1]
간행물
Proceedings of the Tenth ACM SIGPLAN International Conference on Functional Programming (ICFP '05)
http://www.dicta.org[...]
2011-06-22
[2]
서적
The New Hacker’s Dictionary
MIT Press
[3]
웹사이트
bogosort
https://xlinux.nist.[...]
2020-11-11
[4]
간행물
Proceedings of the Third International Conference on Logic Programming
Springer-Verlag
[5]
간행물
4th International Conference on Fun with Algorithms, Castiglioncello, Italy, 2007
http://www.hermann-g[...]
Springer-Verlag
2007
[6]
웹사이트
Google Code Jam 2011, Qualification Rounds, Problem D
https://github.com/g[...]
[7]
웹사이트
Bogobogosort
http://www.dangermou[...]
[8]
arXiv
How inefficient can a sort algorithm be?
[9]
학술지
Quantum Bogosort
https://mathnews.uwa[...]
2009-10-23
[10]
웹사이트
Miracle Sort
https://www.thecshan[...]
2022-09-09
[11]
웹사이트
Intelligent Design Sort
https://www.dangermo[...]
2024-11-06
[12]
웹사이트
http://catb.org/~esr[...]
[13]
간행물
Sorting the Slow Way: An Analysis of Perversely Awful Randomized Sorting Algorithms
http://www.tcs.ifi.l[...]
[14]
웹사이트
http://catb.org/~esr[...]
[15]
인용
Proceedings of the Tenth ACM SIGPLAN International Conference on Functional Programming (ICFP '05)
http://www.dicta.org[...]
2013-03-31
[16]
서적
The New Hacker’s Dictionary
MIT Press
[17]
인용
Proceedings of the Third International Conference on Logic Programming
Springer-Verlag
[18]
인용
Pruning in logic programming
Department of Computer Science, University of Melbourne
1995-06
[19]
인용
4th International Conference on Fun with Algorithms, Castiglioncello, Italy, 2007
http://www.hermann-g[...]
Springer-Verlag
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com